By Jeff Hwang
The pyschological principle behind hit frequency is a concept called variable-ratio reinforcement, which is generally defined as delivering reinforcement after a target behavior is exhibited a random number of times.
Let's take a slot machine, for example. A gambler sits down at a slot machine and bets $1 a pull. Now as you would expect, most of the time, the gambler will bet $1 and lose, which of course is great for the casino. But if all the gambler does is bet $1 and lose every time, eventually he will quit (and/or go broke) and never want to play again. And so every few spins, the slot machine will reward the gambler with a payoff: $1 here, $1 there; $5 here, $1 there.
And then every once in a long while, the machine will reward the gambler with a big payoff in the form of a jackpot.
Now none of this quite adds up, which is how the house wins in the long run. But the promise of the big payoff, along with the intermittent rewards, is generally enough for the casino to reinforce the target behavior, which is to have the gambler keep betting $1 a pull.
That brings us to our next topic, which is the reinforcement schedule.
Reinforcement Schedules: Variable vs. Fixed
There are two basic types of reinforcement schedules: variable-ratio reinforcement schedules, and fixed-ratio reinforcement schedules.
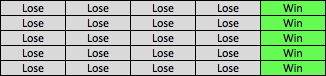
Let's start with the latter, which is the most basic. A fixed-ratio reinforcement schedule is a schedule in which reinforcement is delivered at fixed intervals. Let's say, for example, that you are the casino and you want the slot machine to pay out 20% of the time, or every fifth spin. That is, the gambler will lose $1 four times in a row and get a pyout on the fifth every time.
The reinforcement schedule would look something like this:
Slot Machine: Fixed-Ratio Reinforcement Shedule
The pyschological principle behind hit frequency is a concept called variable-ratio reinforcement, which is generally defined as delivering reinforcement after a target behavior is exhibited a random number of times.
Let's take a slot machine, for example. A gambler sits down at a slot machine and bets $1 a pull. Now as you would expect, most of the time, the gambler will bet $1 and lose, which of course is great for the casino. But if all the gambler does is bet $1 and lose every time, eventually he will quit (and/or go broke) and never want to play again. And so every few spins, the slot machine will reward the gambler with a payoff: $1 here, $1 there; $5 here, $1 there.
And then every once in a long while, the machine will reward the gambler with a big payoff in the form of a jackpot.
Now none of this quite adds up, which is how the house wins in the long run. But the promise of the big payoff, along with the intermittent rewards, is generally enough for the casino to reinforce the target behavior, which is to have the gambler keep betting $1 a pull.
That brings us to our next topic, which is the reinforcement schedule.
Reinforcement Schedules: Variable vs. Fixed
There are two basic types of reinforcement schedules: variable-ratio reinforcement schedules, and fixed-ratio reinforcement schedules.
Let's start with the latter, which is the most basic. A fixed-ratio reinforcement schedule is a schedule in which reinforcement is delivered at fixed intervals. Let's say, for example, that you are the casino and you want the slot machine to pay out 20% of the time, or every fifth spin. That is, the gambler will lose $1 four times in a row and get a pyout on the fifth every time.
The reinforcement schedule would look something like this:
Slot Machine: Fixed-Ratio Reinforcement Shedule
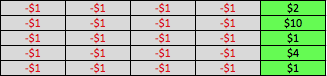
Adjusted for payouts, the schedule might look more like:
Slot Machine: Fixed-Ratio Reinforcment Schedule with Payouts
Slot Machine: Fixed-Ratio Reinforcment Schedule with Payouts
In this scenario, for every 25 spins, the gambler would win $18 on the five winning spins and lose $20 on the rest, for a net loss of $2. For the house, this represents a payout rate of 92% (RTP) and thus a house edge of 8%, which isn't too far from the real thing, depending on what casino you are in.
Now all of this sounds great, but there is a major problem: Nobody would ever play a game with a payout (reinforcement) schedule like this one!
Ok, so maybe "nobody" and "ever" might be a little strong, but the point remains: It wouldn't take long for the gambler to figure out that this slot machine pays out every fifth spin, and only every fifth spin. And as a result, the gambler would eventually quit playing on the spins they know they are going to lose (assuming the payout amounts are still random, meaning that the location of the $10 payout on the schedule is either random or unknown, for example).
Using a variable ratio is the fix for this problem.
Variable-Ratio Reinforcement Schedule
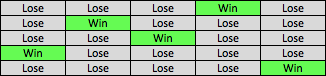
A variable-ratio reinforcment schedule uses a predetermined ratio while delivering the reinforcement randomly. Going back to the slot machine, let's say that you once again are the casino and want the slot machine to pay out 20% of the time, or every fifth time on average.
Now your reinforcement schedule may look something like:
Slot Machine: Variable-Ratio Reinforcement Schedule
Now all of this sounds great, but there is a major problem: Nobody would ever play a game with a payout (reinforcement) schedule like this one!
Ok, so maybe "nobody" and "ever" might be a little strong, but the point remains: It wouldn't take long for the gambler to figure out that this slot machine pays out every fifth spin, and only every fifth spin. And as a result, the gambler would eventually quit playing on the spins they know they are going to lose (assuming the payout amounts are still random, meaning that the location of the $10 payout on the schedule is either random or unknown, for example).
Using a variable ratio is the fix for this problem.
Variable-Ratio Reinforcement Schedule
A variable-ratio reinforcment schedule uses a predetermined ratio while delivering the reinforcement randomly. Going back to the slot machine, let's say that you once again are the casino and want the slot machine to pay out 20% of the time, or every fifth time on average.
Now your reinforcement schedule may look something like:
Slot Machine: Variable-Ratio Reinforcement Schedule
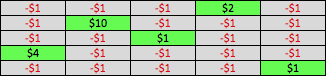
And adjusted for payouts:
Slot Machine: Variable-Ratio Reinforcement Schedule with Payouts
Slot Machine: Variable-Ratio Reinforcement Schedule with Payouts
In aggregate, the expectation is the same: Over 25 spins, the gambler will still net a $2 loss, again giving the casino a 92% payout rate and an 8% house advantage. But in reality, this scenario is far, far more likely to achive the desired result, which is to have the gambler keep playing. Because in contrast to the fixed-ratio reinforcement schedule, a variable-ratio reinforcement schedule with a 20% reinforcement ratio allows for clusters of payouts (e.g. back-to-back wins), as opposed to having spins (or blocks of spins) where the gambler can say for certain that he would lose, and quit playing as a result.
This is because the variable ratio does not specify when the payouts occur, only how often they occur on average.
That said, variable-ratio reinforcement is a concept with endless practical application. As some of you may have noticed, the above discussion came directly from the opening of my book Advanced Pot-Limit Omaha Volume II: LAG Play; in that book, the discussion was used to set the stage for how we think about adjusting c-bet (continuation bet) frequencies based on our opposition, though the concept applies to virtually any action from 3-betting pre-flop to floating the flop.
But with regard to game design, the concept of variable-ratio reinforcement applies most directly to our two basic forms of hit frequency:
Jeff Hwang is President and CEO of High Variance Games LLC. Jeff is also the best-selling author of Pot-Limit Omaha Poker: The Big Play Strategy and the three-volume Advanced Pot-Limit Omaha series.
This is because the variable ratio does not specify when the payouts occur, only how often they occur on average.
That said, variable-ratio reinforcement is a concept with endless practical application. As some of you may have noticed, the above discussion came directly from the opening of my book Advanced Pot-Limit Omaha Volume II: LAG Play; in that book, the discussion was used to set the stage for how we think about adjusting c-bet (continuation bet) frequencies based on our opposition, though the concept applies to virtually any action from 3-betting pre-flop to floating the flop.
But with regard to game design, the concept of variable-ratio reinforcement applies most directly to our two basic forms of hit frequency:
- Payoff frequency, the traditional measure of hit frequency, and
- Betting frequency, the form of hit frequency which has largely been completely overlooked.
Jeff Hwang is President and CEO of High Variance Games LLC. Jeff is also the best-selling author of Pot-Limit Omaha Poker: The Big Play Strategy and the three-volume Advanced Pot-Limit Omaha series.